📐 qual a soma dos ângulos internos de um triângulo?

e o que isso tem a ver com as startups?

e se tudo der errado?

Quando o assunto é lançar um novo negócio no mercado, ainda acreditamos que desistir é algo ruim e que só faz sentido quando nada deu certo. Você tem coragem de engavetar um projeto que não deu certo neste momento, mas que pode dar certo depois?

---

um salve à internet!

Se estamos aqui é por conta da ARPANET, primeiro link de comunicação entre dois computadores remotos... isso aconteceu no dia 29 de outubro de 1969 (mesmo ano que o homem pisou na lua e do nascimento do DJ britânico Roni Size).

Eu imagino as conversas de corredor ao redor do projeto da ARPANET, a quantidade de gente que acreditava ser loucura dois computadores (que na época tinham o tamanho de um quarto e um armazenamento de poucos megabytes). Essa sensação de "loucura" é reflexo natural quando se trata de algum salto tecnológico.

O avanço tecnológico ainda espanta muita gente, especialmente quando pensamos nesse desenvolvimento atrelado a evolução do digital... o poder das conexões, o armazenamento remoto de dados e a velocidade de processamento de grandes volumes de dados dão origem a ferramentas com capacidade de resolver muitos [e diversos] problemas complexos.

O reflexo direto dessa combinação poderosa está no crescimento de negócios baseados no digital que partem de uma base desassociada aos conceitos formais de negócio, ou seja, saem da visão cartesiana para algo que orbita em outras dimensões do racional.

---

📐 qual a soma dos ângulos internos de um triângulo?

Talvez você não saiba, mas minha formação é em matemática, período que descobri e refleti sobre coisas que saiam do que entendia como verdade absoluta... a exemplo da geometria que aprendemos (e que ensinei por anos) na escola.

Segundo Euclides (que deu nome à geometria euclidiana), não há uma definição formal para ponto, reta e plano, isso dá margem à muitas interpretações que [provavelmente] nunca fizemos na escola... mas eu fiz e entendi na universidade.

a soma dos ângulos internos de qualquer triângulo é 180º... se você não lembra, te disseram isso na escola... mas será que essa resposta está 100% certa?

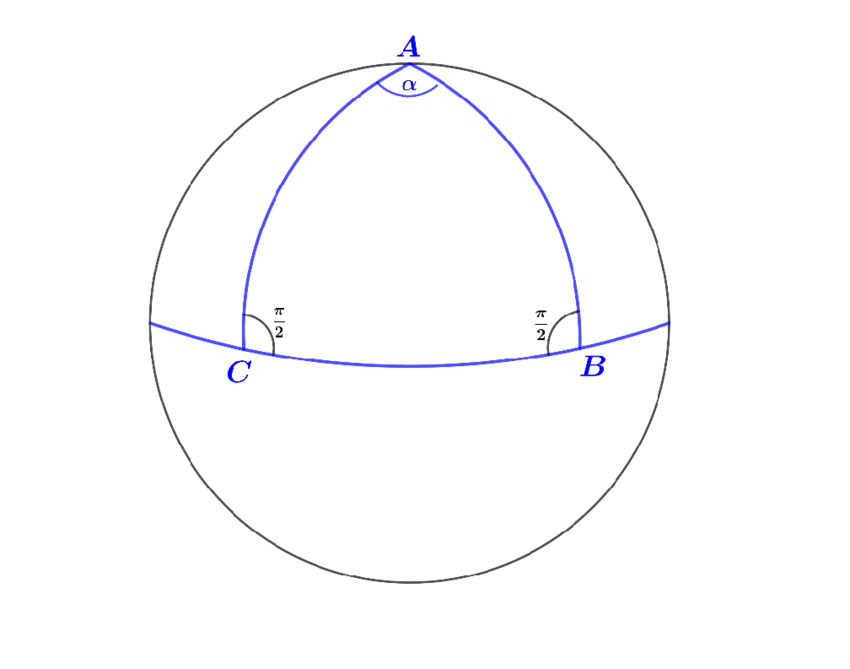
E se considerarmos o "plano" como a superfície de uma esfera, será que as regras de Euclides se aplicam nesse contexto? Se o plano for uma esfera, as retas serão "arcos" e, dessa forma, tudo que aprendemos na escola pode ser questionado, inclusive a soma dos ângulos internos de um triângulo.

Há algum tempo vi uma curiosa pergunta feita por Elon Musk às pessoas que quer contratar:

*“You're standing on the surface of the earth. You walk one mile south, one mile west, and one mile north. You end up exactly where you started. Where are you?”

"Você está na superfície da terra (vamos imaginar que seja uma esfera). Você caminha uma milha para o sul, uma milha para oeste, e uma milha para o norte. Você termina exatamente onde começou. Onde você está?"*

A resposta é: em qualquer lugar da terra (ou de uma esfera perfeita)!

Mas como isso é possível?

No "plano esférico" as regras da geometria euclidiana perde força, consequentemente tudo que aprendemos (ou decoramos) na escola.

O que essa história toda tem a ver com nosso tema central, startups?

Quando falamos sobre o desenvolvimento de startups há um comportamento comum de buscar e seguir por padrões que permitem alcançar objetivos estratégicos, o problema de seguir todas as regras conforme são apresentadas é deixar de lado o nosso contexto.

Euclides estava certo, há um imenso legado matemático construído sobre a geometria euclidiana, mas essa interpretação da geometria não é a única que faz sentido... por sinal uma das minhas pesquisas universitárias era sobre a geometria não-euclidiana, provando teoremas geométricos baseado em outros contextos.

O papel do contexto no desenvolvimento de startups é o que cria a identidade do negócio imerso no mercado, ou seja, para cada problema identificado e entendido como relevantes, há diversas formas de resolvê-lo, tudo vai depender do entendimento de contexto.

---

💻 algumas referências para o final de semana

. O álbum New Forms de Roni Size é excelente para relaxar lendo um livro ou tomando um café;

. O facebook, maior fonte de desinformação, está cavando a própria cova;

. Amazon passou a FedEx no volume de itens transportados nos EUA;

. Essa rádio de bossa nova no YouTube é uma das melhores que já encontrei;

. Presenteei um amigo com o livro "sem esforço" do Greg McKeown.

---

🤗 agradecimento

Obrigado por ter lido mais uma edição da nossa newsletter Sobre Startups... e, se você achar válido, compartilha essa edição com quem não pode deixar de ler sobre o que falamos hoje 🤩

💻 Ah! Aqui você acha mais informações sobre mim 🤗